Connor Smyth
Learning Music Theory
I’ve been learning music theory this year and wanted to share some of my insights and specific learnings that I thought might be useful.
A little history of music and me
I have been playing music on-and-off-since I was about eight years old. It began when my Dad gave me his old 1970s/80s (I don’t know the exact date of purchase) El Degas nylon string acoustic. He later on gave me his Fender Stratocaster El Degas replica from the same era. I still have and play these guitars today with the same Line 6 amp my Grandmother gave me when my Dad gave me the electric guitar. I loved the sound of them and was addicted to trying to learn to play. But, partly due to the size of the guitars in comparison to myself and the lack of knowing what to learn next after learning a few major and minor chords, I never really progressed too far.
Then when I was in middle school I played the trombone and was first introduced to the basics of music theory. The trombone was one of the few instruments in the class that were on the bass clef so playing it was different than the majority of trumpets, saxophone, clarinets, and flutes in class. I even joined the school band and being the only trombonist, I can say that I was the best in category (this doesn’t mean I was actually any good). But I eventually stopped playing that and stopped any further learning about music theory. Do you want to know why? Because the trombone is really heavy and loud. I would have to carry it home regularly and go out to our garage and practice if I wanted to get better. Living in Canada this means that I could essentially not practice at all in winter. In hindsight maybe I should have picked something that was smaller and could be muffled.
I continued to try to further my skills in guitar on and off throughout the years but always hit the point of not knowing how to proceed once I mastered a few chords. I learned a bit more from a friend who is a musician and would wax lyrical about music theory but I could only ever absorb so much before we would quickly go over my head.
Fast-forward to December 2020 where I was at home over the holidays and had a lot of time on my hands. I decided to pick up the guitar again (surprise, surprise…), except this time I have not put it down. Why? Because I decided to learn music theory. My musician friend and I were discussing my recent guitar playing and my attempts to learn cursory theory through observation of what I was playing. He recommended that I read Harmony and Theory by Kieth Wyatt and Carl Shroeder. He warned me that it was dense but as some who read this may know, I read text books for fun. Dense is my forté.
My observations
I am now 36% through the book and I have made a lot of observations that are mostly centred in a mathematical perspective of things. As my friend loves to say “Music is just beautiful math”.
I do want to preface that this is not meant as a message to say that we should rethink the entire way we think about Western music, rather this is a just an alternative way of looking at music for those who are math oriented. I recognize that the way which we communicate about music has been developed and refined over a long period of time and I do not wish to say we should throw it all out. This is just an alternative perspective.
Not everyone has the luxury of sitting down in front a piano or pulling up an image of a piano to think things through may be impractical at that moment in time. This way of thinking about music theory allows you to decouple yourself from any particular instrument and just think about it from a mathematical perspective (but as we’ll find out later on this system does lend itself better to guitar or any other fretted string instrument). You can think of it as learning instrument agnostic music theory.
Western music and the duodecimal system
The dozenal system, otherwise known as base-12 or duodecimal, is a very interesting system of counting for many reasons. If you want to find out a bit more about it, then I recommend checking out this Numberphile, video:
The quick version of the duodecimal system is that rather than starting at 0 and counting to 9, then starting the system over again with 10 (i.e. 0, 1, 2, 3, … , 9, 10, 11, 12, 13,…) you start with 0 count to 11, and then start the system all over again. The duodecimal number system goes as follows,
0 1 2 3 4 5 6 7 8 9 X Ɛ
10 11 12 13 14 15 16 17 18 19 1X 1Ɛ
20 21 22 23 24 25 26 27 28 29 2X 2Ɛ
…
There a numerous benefits to using this system of counting and if you’re curious I recommend watching the video or researching the system for yourself but among them are that the system matches perfectly to the Western style of music which is based around the C major scale.
You can see in the image below one example of how it maps to the system. The example below is a duodecimal clockface as in the logo of the Dozenal Society of America, here used to denote musical keys.
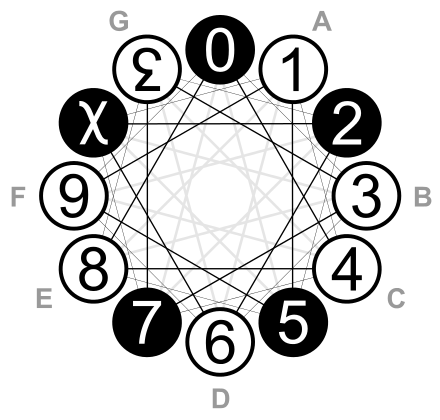
The system maps better when you correspond the numbers to specific tones:
| C | C# | D | D# | E | F | F# | G | G# | A | A# | B |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | Ɛ |
Anyone who is familiar with a bit music theory may notice that this is a much easier way to think. In music theory we say that a major triad is made up of the root (first), third, and fifth notes of the major scale. But to someone who is not familiar with music theory you might think that a C major triad is then C, C#, and D; that is not a C major triad.
The C major triad is made up of 8 notes (including the octave) which are C, D, E, F, G, A, B, and C. Thus the C major triad is actually C, E, and G (1, 3, and 5). This same pattern applies to each major scale, so if we were to look at the A major scale it would be A, B, C#, D, E, F#, G#, and A. Then the A major triad would be A, C#, and E. All of this requires you to know the specific scales and there are a lot of scales to try to remember.
If you’re fairly perceptive, then you may have noticed a pattern based on the two examples I have provided you: the major triads are made up of the 0, 4, and 7 notes when you look at all 12 tones (or 10 if you’re counting in base-12).
The same applies to all of the scales no matter the tonic (the tonic is the first scale degree, ex. C in C major).
| A | A# | B | C | C# | D | D# | E | F | F# | G | G# |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | Ɛ |
| F# | G | G# | A | A# | B | C | C# | D | D# | E | F |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | Ɛ |
This system can also be used for all other scales/modes. For the minor scale for example, all you have to do is change the 4 to a 3 since a minor triad is the same as a major just with the third degree stepped down a half step.
| G | Ab | A | Bb | B | C | Cb | D | Db | E | F | Fb |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | Ɛ |
Using the duodecimal system for counting
If you’re just starting to learn about music theory one of the most difficult things in my experience can be understanding and using intervals. This is because the English alphabet does not contain half-steps like the Western music scale does. In music theory what you are really trying to do is count to 12 (or 10 if you are looking at it in the duodecimal system) but with a jumble of letters and “special” letters. If you were to use numbers and translate them to the appropriate letters in the musical scales then your life may become a lot easier.
One of the biggest limitations is that you have only 5 fingers on each hand, so unless you want to pull out a pad of paper or grow a few extra fingers here is how some places in the world count using only one hand.
In the diagram below you can see how you can use the segments of your fingers to count from 0-Ɛ or optionally 1-10 (10 being the duodecimal equivalent to 12). If I am losing you with how the duodecimal system works then you should scroll up a bit and watch the video I posted (even if you already watched it). This counting system can also be used once you begin to master the intervals and only wish to count the notes that occur in a diatonic scale (i.e 0-7 or 1-8).

Duodecimal system and the fretboard
If you are familiar with a fretted instrument such as the guitar you will have noticed something neat about this counting system. It directly maps to a fretboard. I will use a guitar for my examples here since that is what I am most familiar with.
The notes on the frets of a guitar repeat at 12 (i.e. an open E string and the 12th fret of the E string are both E notes, the latter is just one octave higher). So if we think of the open strings as being 0 and the 11th fret as being Ɛ, then you can see how it perfectly maps. Below I will show you what I mean.
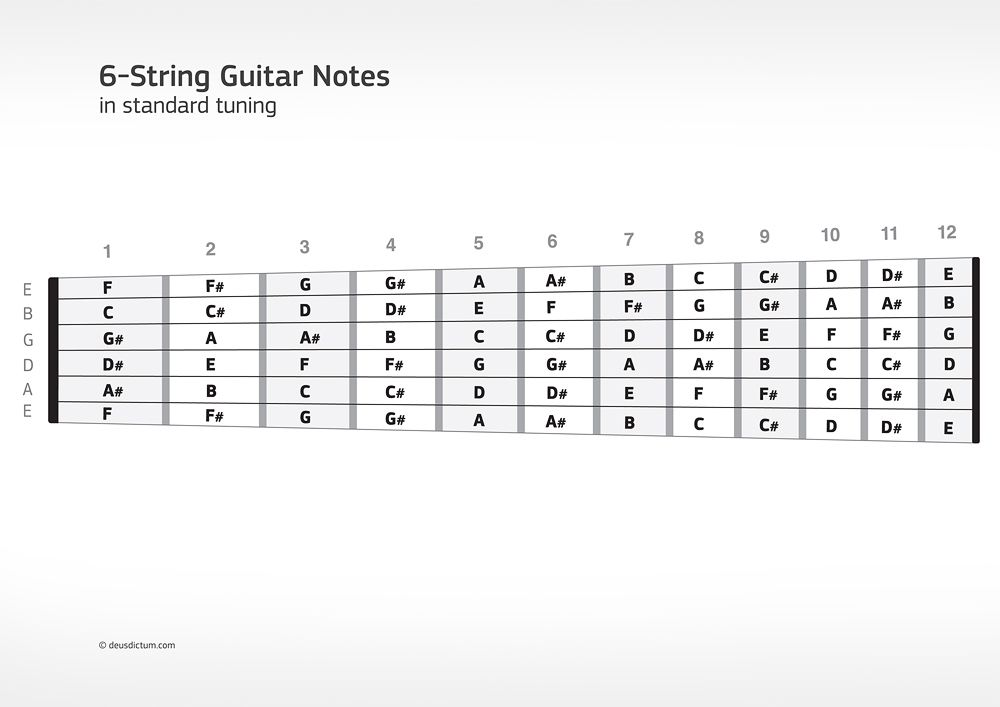
Here you can see that for each string, the open string is the root, the fourth fret is always the 3rd degree in the triad and the seventh fret is always the fifth degree in the triad. Using this method can help make it a lot easier to memorize the fretboard in terms of notes and can help you memorize barre chords moving up or down the fretboard.
Circle of Fifths formula
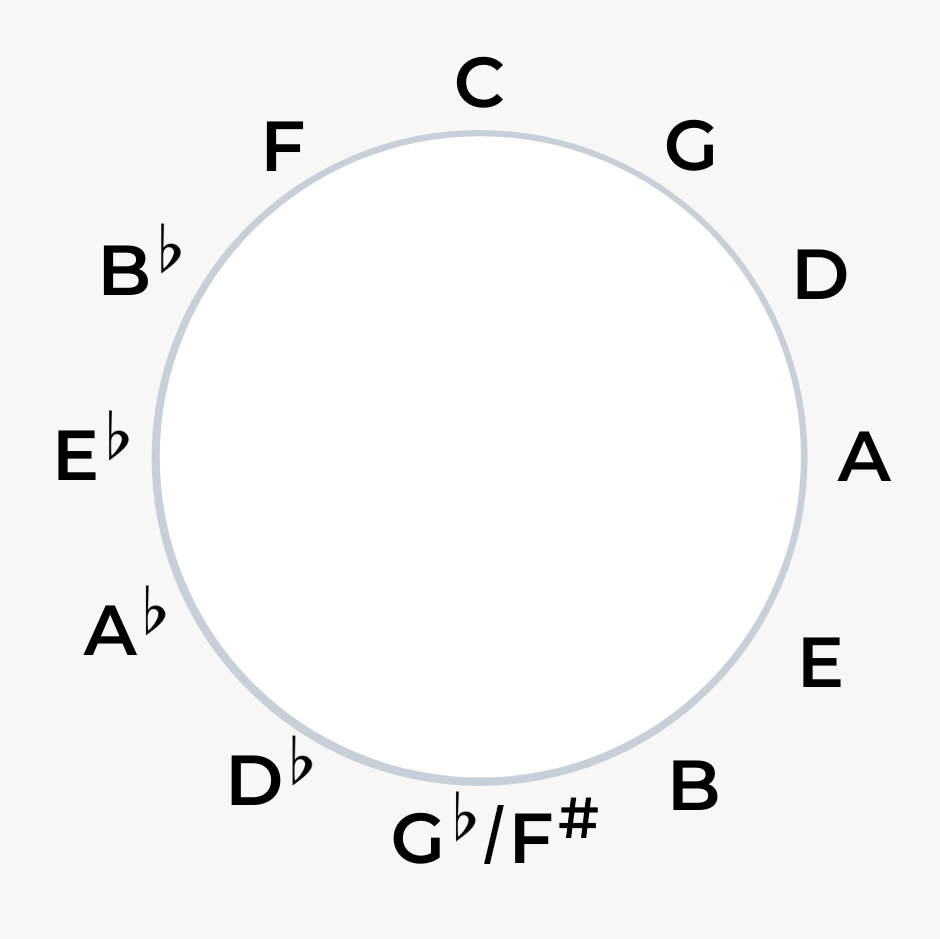
The circle of fifths follow a mathematical pattern that once applied to the duodecimal system makes it far easier to understand and comprehend as to why it works. Well actually it has two formulas depending on whether you wish to view it as repeating or incrementing.
If you wish to view it as repeating and you begin with 0, then the set is as follows:
In decimal,
{ 0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, … }
In base-12,
{ 0, 7, 2, 9, 4, Ɛ, 6, 1, 8, 3, X, … }
If you wish to view it as incrementing and you begin with 0, then the set is as follows:
In decimal,
{ 0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, … }
In base-12,
{ 0, 7, 12, 19 24, 2Ɛ, 36, 41, 48, 53, 5X, … }